Floating point precision, in practice

Normally as a programmer Float’s are more than precise enough. During one of my projects however I had some serious headaches because of it. At start of the project I was rolling my own points in 3D-space, just a fancy wrapper around 3 Doubles. When I needed more vector powers (cross products, quaternations, rotation matrices) I switched to com.github.jpbetz.subspace.Vector3 from https://github.com/jpbetz/subspace. This Vector3 uses 3 Floats internally, which was fine, cause it wouldn’t make that much of a difference, I thought.

The project I’m working on includes fitting some points to a predefined shape (a inline skate track to be precise). I was calculating the center of the GPS input like this:

val vs: Seq[Vector3] = /* about 3600 points */ ???
val center = vs.reduce(_ + _) / vs.size

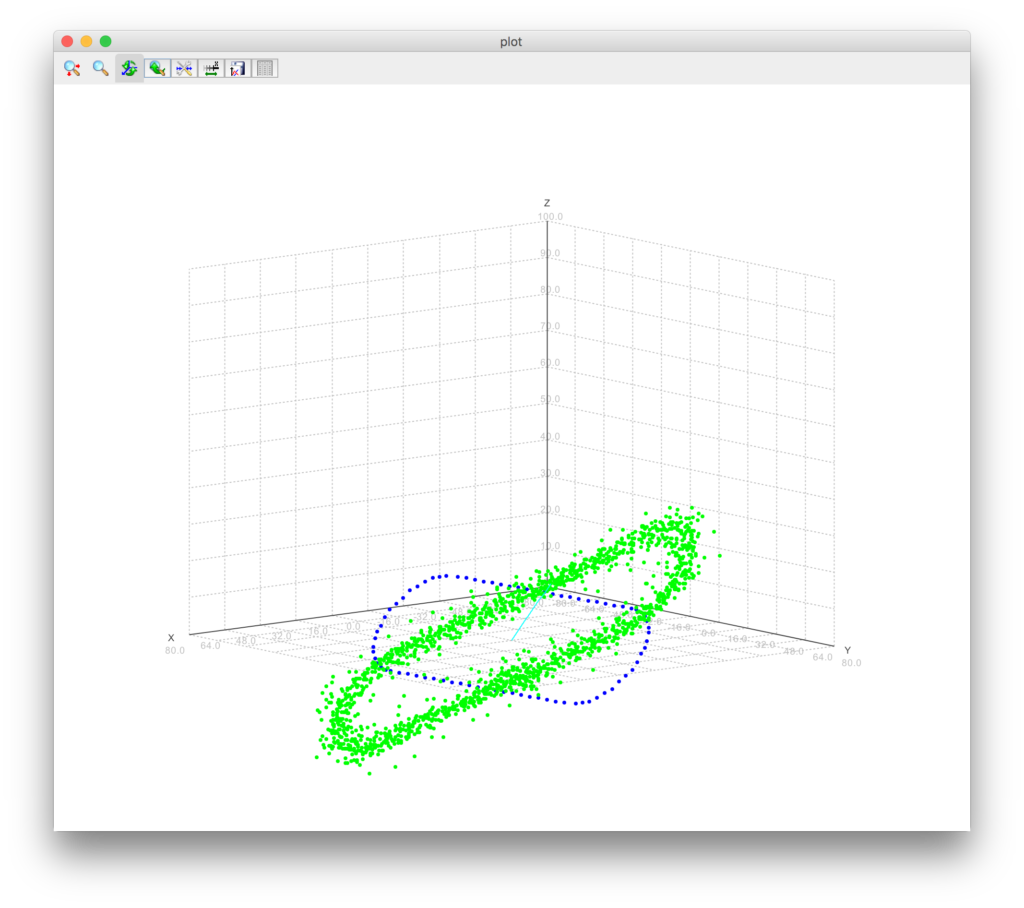
Using this center I plotted a blue ‘perfect’ track and my input points in green. The result: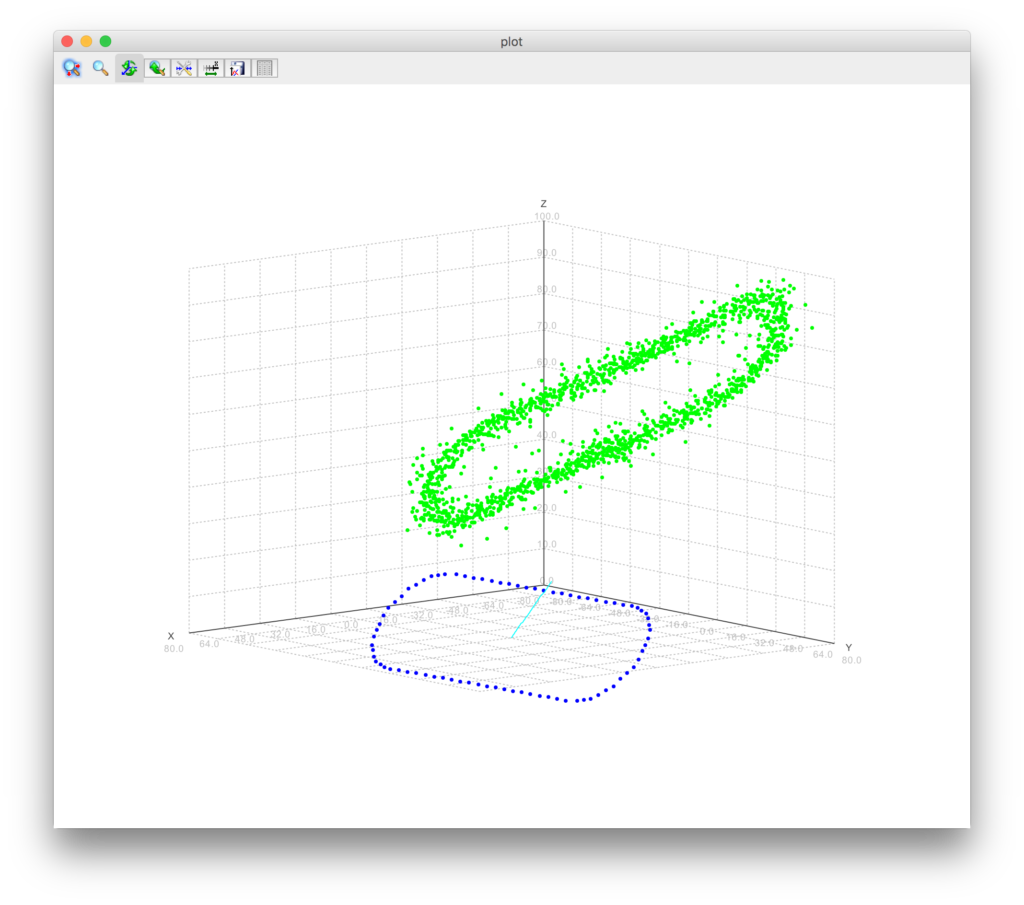

As you can see there is some offset between the green and the blue tracks. The orientation is different too, but first I wanted to fix the positioning problem. After many hours of thinkering and continuing with other issues, I came across another issue with my Floats: the formatting back to GPS longitude and latitudes. For some reason I wrongly typed the formatting string, but due to this issue my attention shifted to floating point precision and it’s quirks. Then I wrote this little test:

val sum_d = vs
  .map(v => (v.x.toDouble, v.y.toDouble, v.z.toDouble))
  .reduce((a,b) => (a._1+b._1, a._2+b._2, a._3+b._3))
val center_d = Vector3(
  (sum_d._1/vs.size).toFloat,
  (sum_d._2/vs.size).toFloat,
  (sum_d._3/vs.size)).toFloat
)
var center = vs.reduce(_ + _) / vs.size
println(s"Center: $center")
println(s"Center using doubles: $center_d")
println(s"Diff: ${center - center_d}")

which printed

Center: (3912099.2, 301133.1, 5028436.0)
Center using doubles: (3912057.8, 301132.88, 5028494.5)
Diff = (41.5, 0.21875, -58.5)

Tada! Issue found. Adding all those large numbers (vectors relative to the earths center) caused the precision of the resulting float to be too little to accomodate for the large numbers plus their precision. Using doubles to store the accumulating numbers results in a better center, which produces the following image:

Much better! So remember, floats are not always good enough.